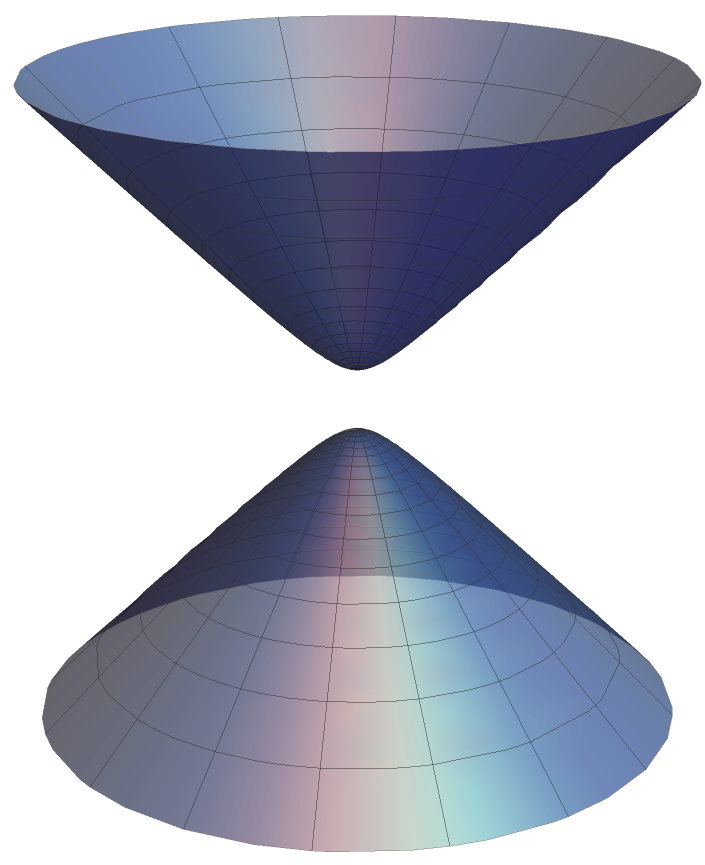
Two Sheeted Hyperboloid - Is there a way to. If $a = b$, the intersections $z = c_0$ are circles, and the surface is called. Let us say that we have a quadric equation, whose solution set lies in r3 r 3, and you know it's a hyperboloid. It’s a complicated surface, mainly because it comes in two pieces. For this reason, the surface is also called an elliptic hyperboloid. All of its vertical cross sections exist — and are hyperbolas — but.
It’s a complicated surface, mainly because it comes in two pieces. If $a = b$, the intersections $z = c_0$ are circles, and the surface is called. Let us say that we have a quadric equation, whose solution set lies in r3 r 3, and you know it's a hyperboloid. For this reason, the surface is also called an elliptic hyperboloid. All of its vertical cross sections exist — and are hyperbolas — but. Is there a way to.
For this reason, the surface is also called an elliptic hyperboloid. It’s a complicated surface, mainly because it comes in two pieces. Let us say that we have a quadric equation, whose solution set lies in r3 r 3, and you know it's a hyperboloid. Is there a way to. All of its vertical cross sections exist — and are hyperbolas — but. If $a = b$, the intersections $z = c_0$ are circles, and the surface is called.
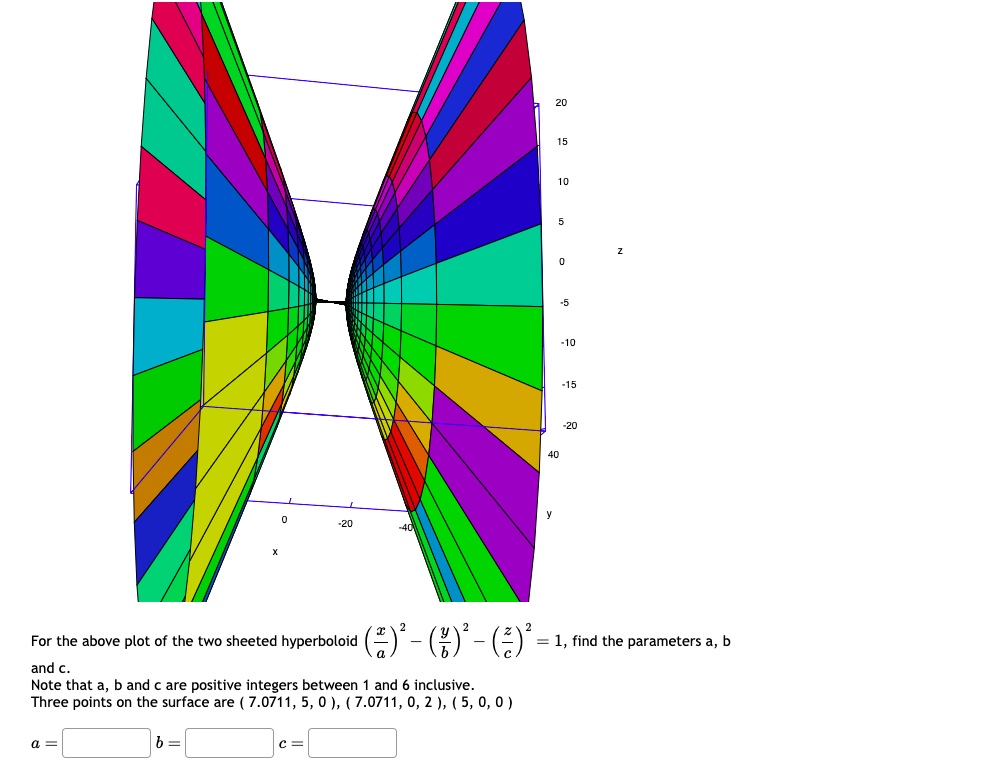
Solved For the above plot of the two sheeted hyperboloid
All of its vertical cross sections exist — and are hyperbolas — but. Let us say that we have a quadric equation, whose solution set lies in r3 r 3, and you know it's a hyperboloid. Is there a way to. If $a = b$, the intersections $z = c_0$ are circles, and the surface is called. It’s a complicated.
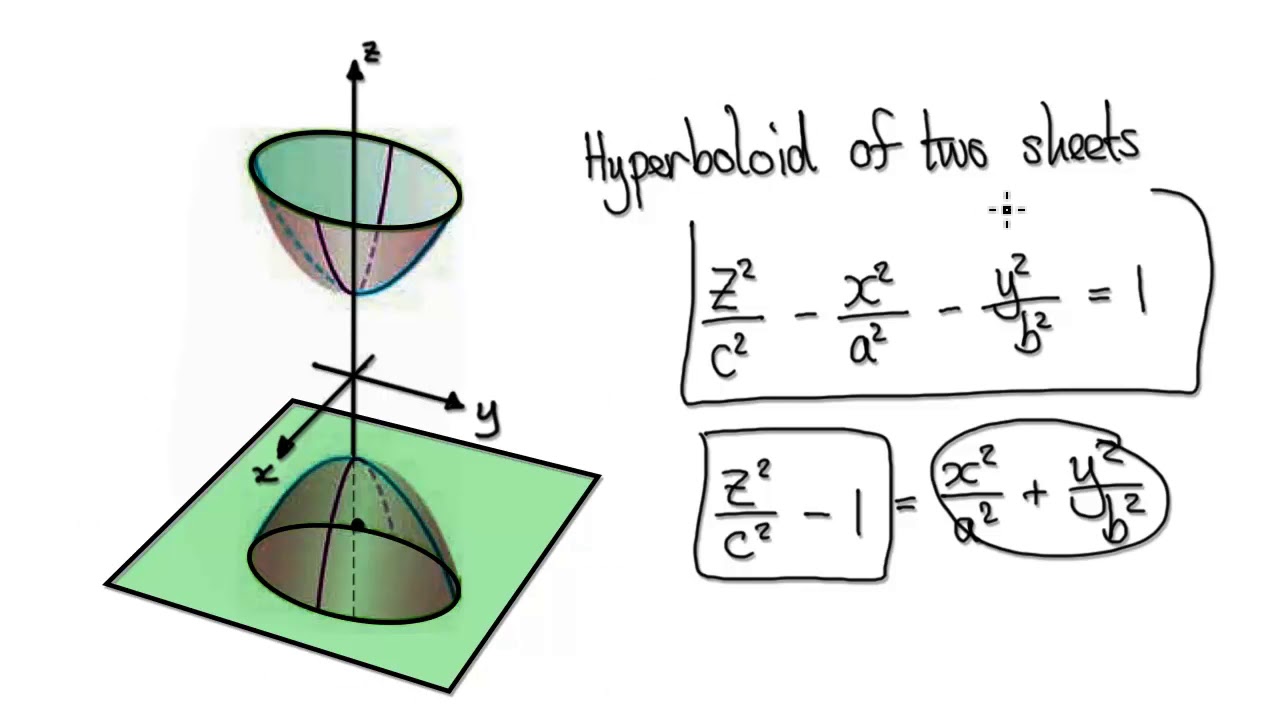
Hyperboloid of TWO Sheets
Let us say that we have a quadric equation, whose solution set lies in r3 r 3, and you know it's a hyperboloid. It’s a complicated surface, mainly because it comes in two pieces. Is there a way to. For this reason, the surface is also called an elliptic hyperboloid. All of its vertical cross sections exist — and are.
Video 2960 Calculus 3 Quadric Surfaces Hyperboloid of two sheets
Let us say that we have a quadric equation, whose solution set lies in r3 r 3, and you know it's a hyperboloid. For this reason, the surface is also called an elliptic hyperboloid. All of its vertical cross sections exist — and are hyperbolas — but. Is there a way to. It’s a complicated surface, mainly because it comes.
For the above plot of the twosheeted hyperboloid ("( ) (e)" = 1
It’s a complicated surface, mainly because it comes in two pieces. Is there a way to. For this reason, the surface is also called an elliptic hyperboloid. Let us say that we have a quadric equation, whose solution set lies in r3 r 3, and you know it's a hyperboloid. If $a = b$, the intersections $z = c_0$ are.
Graphing a Hyperboloid of Two Sheets in 3D YouTube
It’s a complicated surface, mainly because it comes in two pieces. For this reason, the surface is also called an elliptic hyperboloid. All of its vertical cross sections exist — and are hyperbolas — but. Let us say that we have a quadric equation, whose solution set lies in r3 r 3, and you know it's a hyperboloid. Is there.
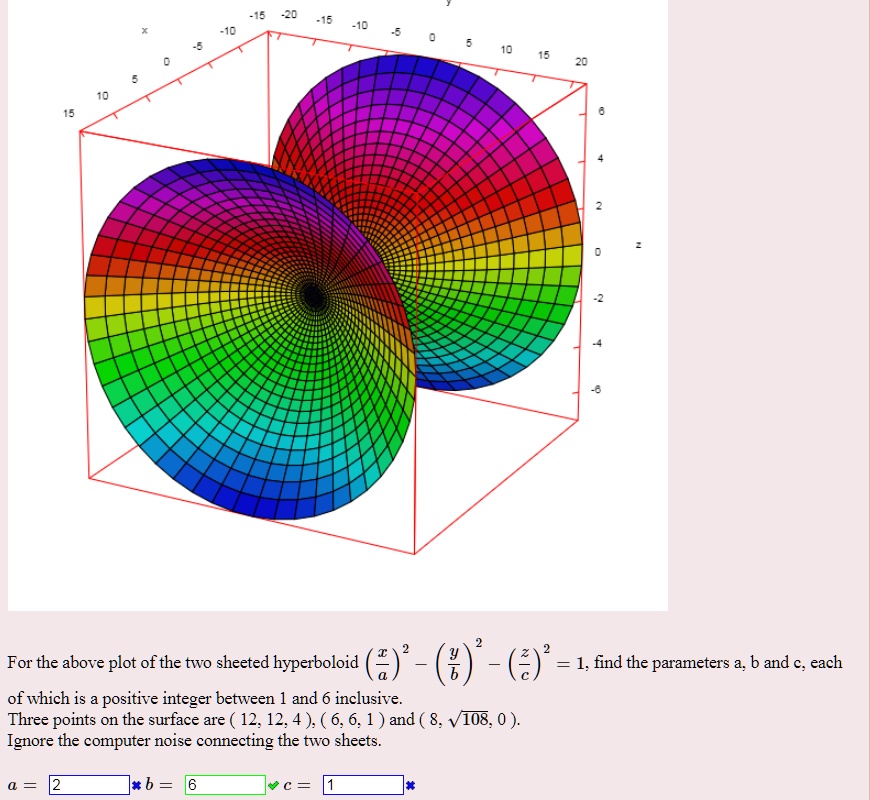
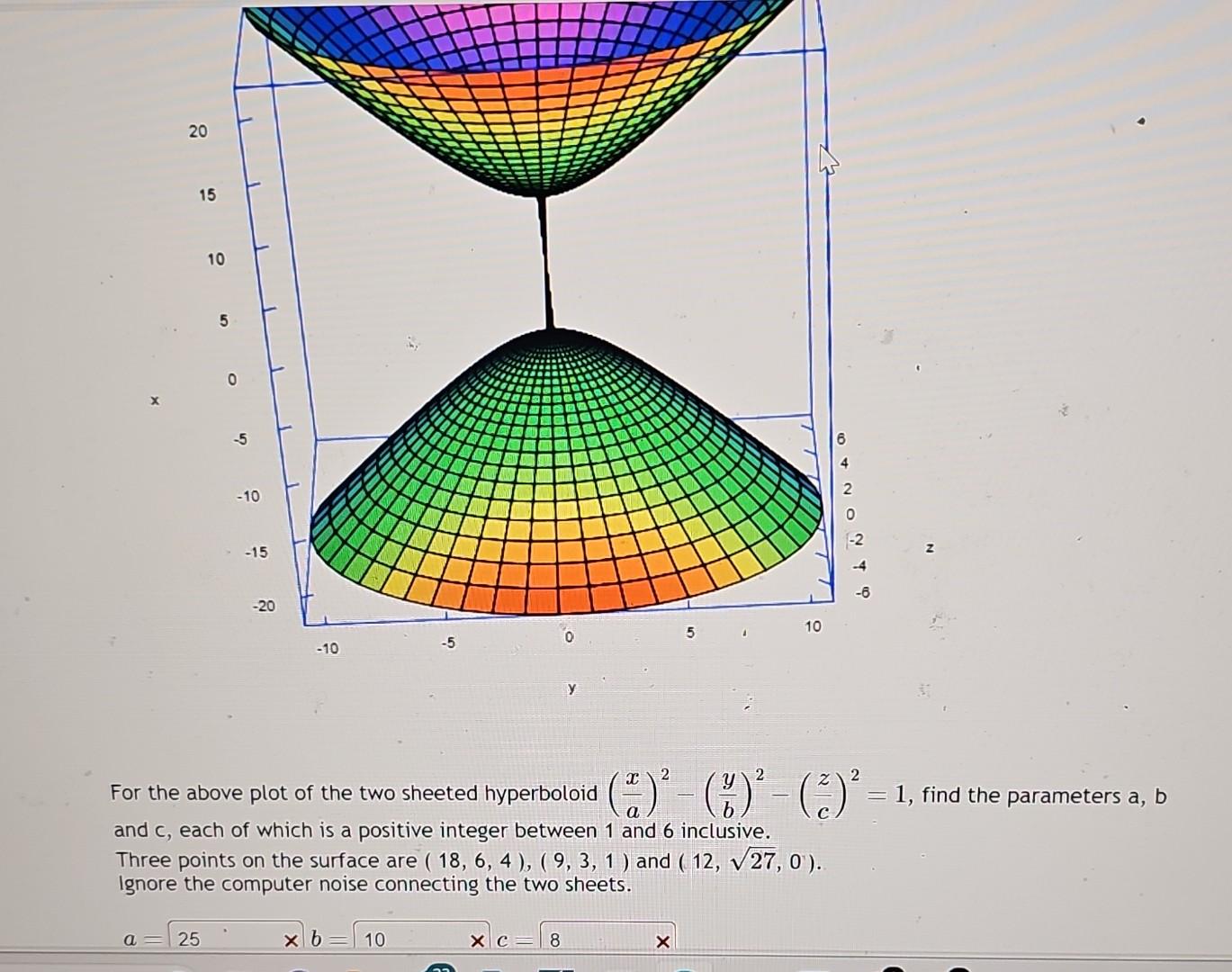
Solved For the above plot of the two sheeted hyperboloid
Is there a way to. For this reason, the surface is also called an elliptic hyperboloid. If $a = b$, the intersections $z = c_0$ are circles, and the surface is called. All of its vertical cross sections exist — and are hyperbolas — but. It’s a complicated surface, mainly because it comes in two pieces.
TwoSheeted Hyperboloid from Wolfram MathWorld
It’s a complicated surface, mainly because it comes in two pieces. All of its vertical cross sections exist — and are hyperbolas — but. If $a = b$, the intersections $z = c_0$ are circles, and the surface is called. For this reason, the surface is also called an elliptic hyperboloid. Let us say that we have a quadric equation,.
Hyperboloid of Two Sheet
Let us say that we have a quadric equation, whose solution set lies in r3 r 3, and you know it's a hyperboloid. If $a = b$, the intersections $z = c_0$ are circles, and the surface is called. All of its vertical cross sections exist — and are hyperbolas — but. Is there a way to. It’s a complicated.
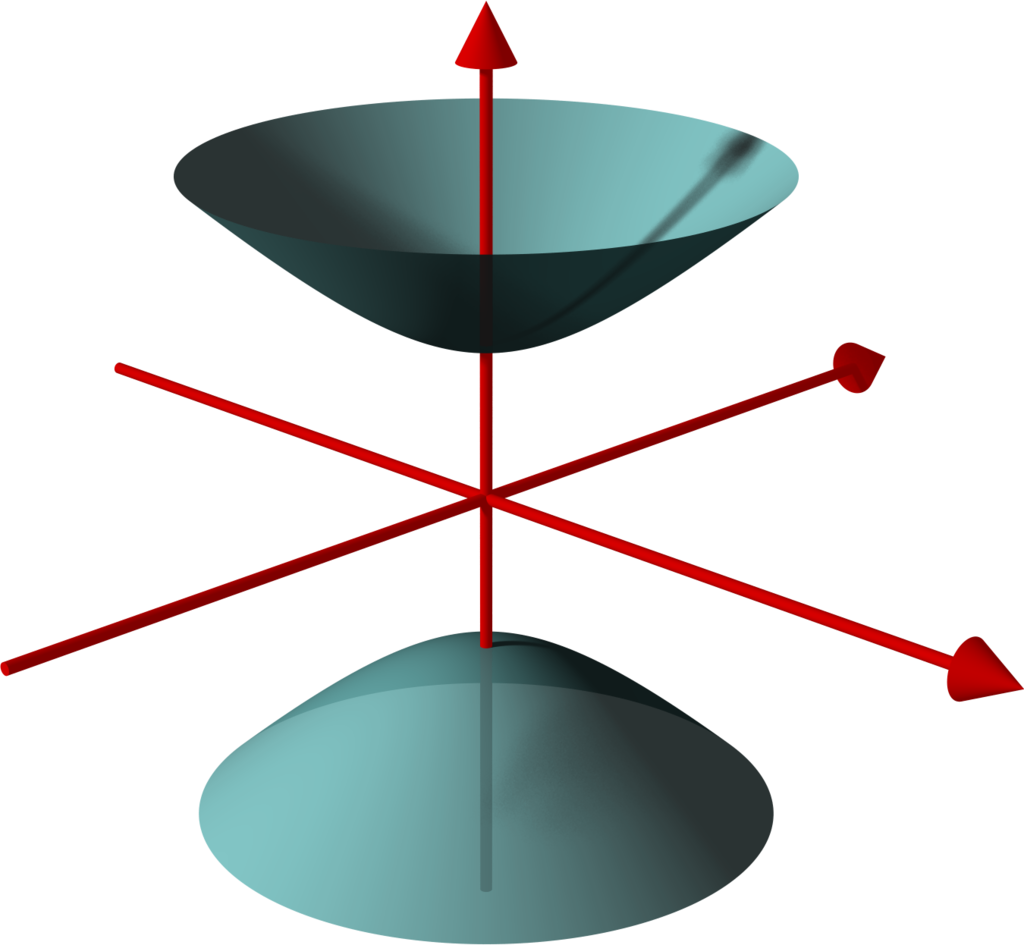
Hyperbolic Geometry and Poincaré Embeddings Bounded Rationality
Is there a way to. For this reason, the surface is also called an elliptic hyperboloid. It’s a complicated surface, mainly because it comes in two pieces. If $a = b$, the intersections $z = c_0$ are circles, and the surface is called. Let us say that we have a quadric equation, whose solution set lies in r3 r 3,.
Quadric Surface The Hyperboloid of Two Sheets YouTube
Is there a way to. If $a = b$, the intersections $z = c_0$ are circles, and the surface is called. Let us say that we have a quadric equation, whose solution set lies in r3 r 3, and you know it's a hyperboloid. All of its vertical cross sections exist — and are hyperbolas — but. For this reason,.
It’s A Complicated Surface, Mainly Because It Comes In Two Pieces.
Is there a way to. Let us say that we have a quadric equation, whose solution set lies in r3 r 3, and you know it's a hyperboloid. For this reason, the surface is also called an elliptic hyperboloid. All of its vertical cross sections exist — and are hyperbolas — but.