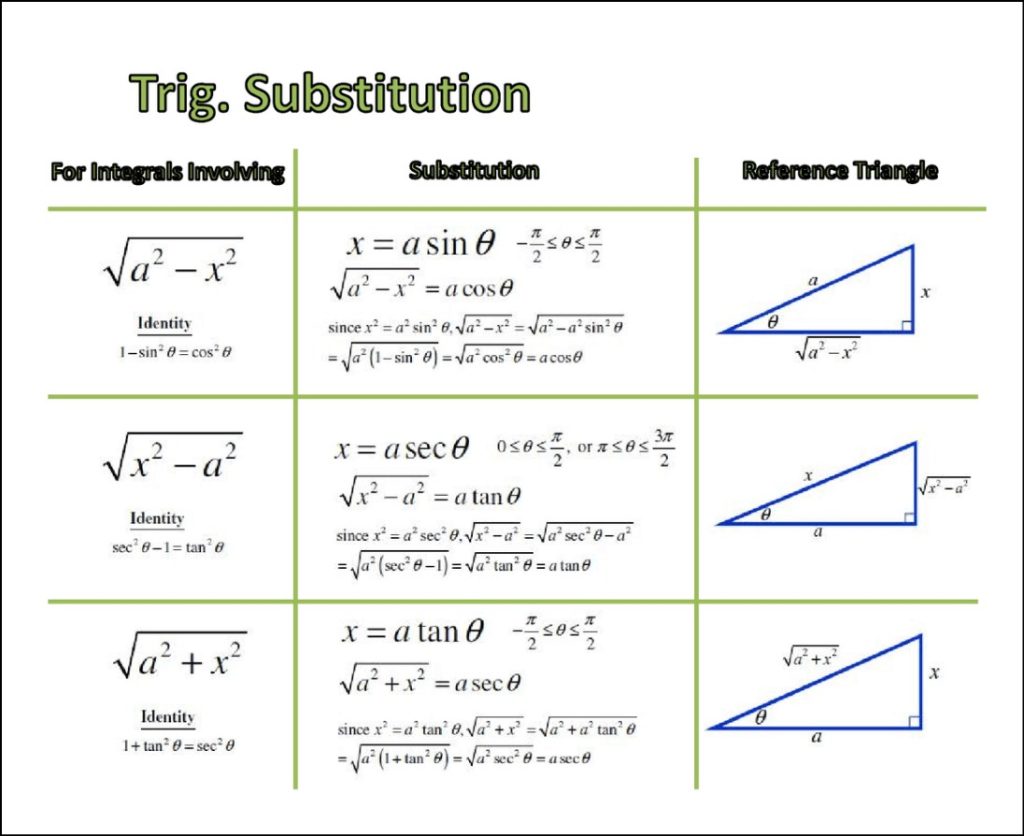
Trig Integrals Cheat Sheet - If the integral contains the following root use the given substitution and formula to convert into an integral involving trig functions. Integral of a constant \int f\left(a\right)dx=x\cdot f\left(a\right) take the constant out \int a\cdot f\left(x\right)dx=a\cdot \int f\left(x\right)dx sum rule \int f\left(x\right)\pm g\left(x\right)dx=\int. N (x)dx (a) if the 2power n of cosine is odd (n =2k + 1), save one cosine factor and use cos (x)=1. R strategy for evaluating sin: Note that θ is often interchangeable with x as a variable,. Integral trigonometry cheat sheet by crossant trigonometric identities and common trigonometric integrals.
R strategy for evaluating sin: If the integral contains the following root use the given substitution and formula to convert into an integral involving trig functions. N (x)dx (a) if the 2power n of cosine is odd (n =2k + 1), save one cosine factor and use cos (x)=1. Integral of a constant \int f\left(a\right)dx=x\cdot f\left(a\right) take the constant out \int a\cdot f\left(x\right)dx=a\cdot \int f\left(x\right)dx sum rule \int f\left(x\right)\pm g\left(x\right)dx=\int. Integral trigonometry cheat sheet by crossant trigonometric identities and common trigonometric integrals. Note that θ is often interchangeable with x as a variable,.
N (x)dx (a) if the 2power n of cosine is odd (n =2k + 1), save one cosine factor and use cos (x)=1. If the integral contains the following root use the given substitution and formula to convert into an integral involving trig functions. Note that θ is often interchangeable with x as a variable,. Integral of a constant \int f\left(a\right)dx=x\cdot f\left(a\right) take the constant out \int a\cdot f\left(x\right)dx=a\cdot \int f\left(x\right)dx sum rule \int f\left(x\right)\pm g\left(x\right)dx=\int. R strategy for evaluating sin: Integral trigonometry cheat sheet by crossant trigonometric identities and common trigonometric integrals.
Trig Substitution Cheat Sheet With Formulas Substitution
Integral trigonometry cheat sheet by crossant trigonometric identities and common trigonometric integrals. Integral of a constant \int f\left(a\right)dx=x\cdot f\left(a\right) take the constant out \int a\cdot f\left(x\right)dx=a\cdot \int f\left(x\right)dx sum rule \int f\left(x\right)\pm g\left(x\right)dx=\int. Note that θ is often interchangeable with x as a variable,. If the integral contains the following root use the given substitution and formula to convert into.
Integral Trigonometry Cheat Sheet by CROSSANT Download free from
Integral of a constant \int f\left(a\right)dx=x\cdot f\left(a\right) take the constant out \int a\cdot f\left(x\right)dx=a\cdot \int f\left(x\right)dx sum rule \int f\left(x\right)\pm g\left(x\right)dx=\int. If the integral contains the following root use the given substitution and formula to convert into an integral involving trig functions. N (x)dx (a) if the 2power n of cosine is odd (n =2k + 1), save one cosine.
Complete table of integrals in a single sheet, Integrals of trig
Integral of a constant \int f\left(a\right)dx=x\cdot f\left(a\right) take the constant out \int a\cdot f\left(x\right)dx=a\cdot \int f\left(x\right)dx sum rule \int f\left(x\right)\pm g\left(x\right)dx=\int. N (x)dx (a) if the 2power n of cosine is odd (n =2k + 1), save one cosine factor and use cos (x)=1. If the integral contains the following root use the given substitution and formula to convert into.
Trigonometry Laws and Identities Cheat Sheet. It includes tangent
Integral trigonometry cheat sheet by crossant trigonometric identities and common trigonometric integrals. R strategy for evaluating sin: Note that θ is often interchangeable with x as a variable,. Integral of a constant \int f\left(a\right)dx=x\cdot f\left(a\right) take the constant out \int a\cdot f\left(x\right)dx=a\cdot \int f\left(x\right)dx sum rule \int f\left(x\right)\pm g\left(x\right)dx=\int. If the integral contains the following root use the given substitution.
Calculus Integrals Reference Sheet (with Formulas) EEWeb
N (x)dx (a) if the 2power n of cosine is odd (n =2k + 1), save one cosine factor and use cos (x)=1. If the integral contains the following root use the given substitution and formula to convert into an integral involving trig functions. R strategy for evaluating sin: Integral of a constant \int f\left(a\right)dx=x\cdot f\left(a\right) take the constant out.
Trig Indefinite Integrals Cheat Sheet PDF
N (x)dx (a) if the 2power n of cosine is odd (n =2k + 1), save one cosine factor and use cos (x)=1. Integral of a constant \int f\left(a\right)dx=x\cdot f\left(a\right) take the constant out \int a\cdot f\left(x\right)dx=a\cdot \int f\left(x\right)dx sum rule \int f\left(x\right)\pm g\left(x\right)dx=\int. R strategy for evaluating sin: Note that θ is often interchangeable with x as a variable,..
Derivative and Integral Cheat Sheet Cheat Sheet Calculus Docsity
N (x)dx (a) if the 2power n of cosine is odd (n =2k + 1), save one cosine factor and use cos (x)=1. R strategy for evaluating sin: Integral trigonometry cheat sheet by crossant trigonometric identities and common trigonometric integrals. Integral of a constant \int f\left(a\right)dx=x\cdot f\left(a\right) take the constant out \int a\cdot f\left(x\right)dx=a\cdot \int f\left(x\right)dx sum rule \int f\left(x\right)\pm.
Trig cheat sheet
N (x)dx (a) if the 2power n of cosine is odd (n =2k + 1), save one cosine factor and use cos (x)=1. Integral of a constant \int f\left(a\right)dx=x\cdot f\left(a\right) take the constant out \int a\cdot f\left(x\right)dx=a\cdot \int f\left(x\right)dx sum rule \int f\left(x\right)\pm g\left(x\right)dx=\int. R strategy for evaluating sin: If the integral contains the following root use the given substitution.
Trigonometry Cheat Sheet Algebra Ii Pre Calculus Trigonometry Cheat
R strategy for evaluating sin: If the integral contains the following root use the given substitution and formula to convert into an integral involving trig functions. N (x)dx (a) if the 2power n of cosine is odd (n =2k + 1), save one cosine factor and use cos (x)=1. Integral trigonometry cheat sheet by crossant trigonometric identities and common trigonometric.
Trig Identities, Tables, Charts and Cheat Sheets
Integral trigonometry cheat sheet by crossant trigonometric identities and common trigonometric integrals. Integral of a constant \int f\left(a\right)dx=x\cdot f\left(a\right) take the constant out \int a\cdot f\left(x\right)dx=a\cdot \int f\left(x\right)dx sum rule \int f\left(x\right)\pm g\left(x\right)dx=\int. N (x)dx (a) if the 2power n of cosine is odd (n =2k + 1), save one cosine factor and use cos (x)=1. If the integral contains.
R Strategy For Evaluating Sin:
If the integral contains the following root use the given substitution and formula to convert into an integral involving trig functions. N (x)dx (a) if the 2power n of cosine is odd (n =2k + 1), save one cosine factor and use cos (x)=1. Integral trigonometry cheat sheet by crossant trigonometric identities and common trigonometric integrals. Integral of a constant \int f\left(a\right)dx=x\cdot f\left(a\right) take the constant out \int a\cdot f\left(x\right)dx=a\cdot \int f\left(x\right)dx sum rule \int f\left(x\right)\pm g\left(x\right)dx=\int.